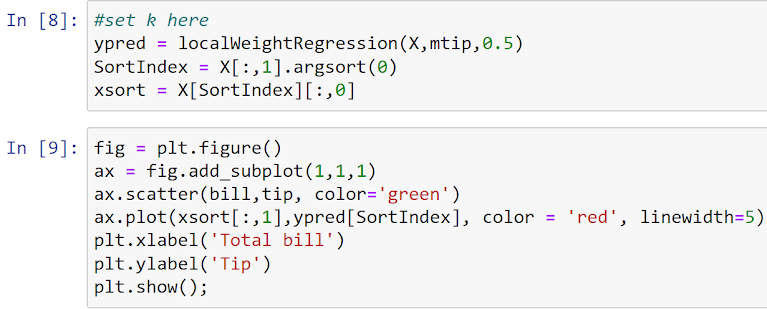
WEEK 10: Implement the non-parametric Locally Weighted Regression algorithm in order to fit data points. Select appropriate data set for your experiment and draw graphs.

Locally Weighted Regression Algorithm

Regression:

· Regression is a technique from statistics that are used to predict values of the desired target quantity when the target quantity is continuous.

o In regression, we seek to identify (or estimate) a continuous variable y associated with a given input vector x.

§ y is called the dependent variable.

§ x is called the independent variable.

Loess/Lowess Regression:

Loess regression is a nonparametric technique that uses local weighted regression to fit a smooth curve through points in a scatter plot.

Lowess Algorithm:

· Locally weighted regression is a very powerful nonparametric model used in statistical learning.

· Given a dataset X, y, we attempt to find a model parameter β(x) that minimizes residual sum of weighted squared errors.

· The weights are given by a kernel function (k or w) which can be chosen arbitrarily

Algorithm

1. Read the Given data Sample to X and the curve (linear or nonlinear) to Y

2. Set the value for Smoothening parameter or Free parameter say τ

3. Set the bias /Point of interest set x0 which is a subset of X

4. Determine the weight matrix using:

5. Determine the value of model term parameter β using:

6. Prediction = x0*β

Python Program to Implement and Demonstrate Locally Weighted Regression Algorithm

Machine Learning