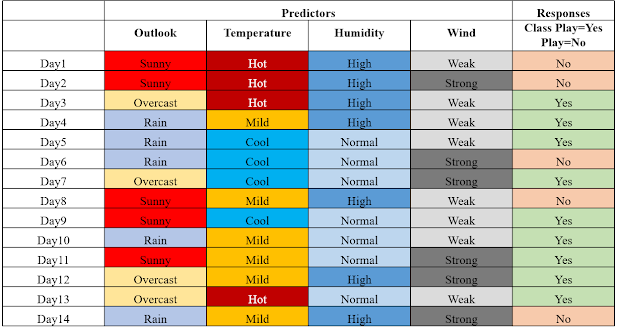
Naive Bayes Classifier - Example -classify- play tennis - forecast

Naïve Bayes Classifier - Example -classify- play tennis - forecast

Let’s build a classifier that predicts whether I should play tennis given the forecast.
It takes four attributes to describe the forecast; namely,

the outlook,
the temperature,
the humidity, and
the presence or absence of wind.

Furthermore, the values of the four attributes are qualitative (also known as categorical).
They take on the values shown below.

𝑶𝒖𝒕𝒍𝒐𝒐𝒌 ∈[𝑺𝒖𝒏𝒏𝒚,𝑶𝒗𝒆𝒓𝒄𝒂𝒔𝒕, 𝑹𝒂𝒊𝒏𝒚]
𝑻𝒆𝒎𝒑𝒆𝒓𝒂𝒕𝒖𝒓𝒆∈[𝑯𝒐𝒕,𝑴𝒊𝒍𝒅, 𝑪𝒐𝒐𝒍]
𝑯𝒖𝒎𝒊𝒅𝒊𝒕𝒚 ∈[𝑯𝒊𝒈𝒉, 𝑵𝒐𝒓𝒎𝒂𝒍]
𝑾𝒊𝒏𝒅𝒚 ∈[𝑾𝒆𝒂𝒌, 𝑺𝒕𝒓𝒐𝒏𝒈]

The class label is the variable, Play and takes the values Yes or No.

𝑷𝒍𝒂𝒚∈[𝒀𝒆𝒔, 𝑵𝒐]

We read-in training data below that has been collected over 14 days

Classification Phase

Let’s say, we get a new instance of the weather condition,

𝑿^′=(𝑶𝒖𝒕𝒍𝒐𝒐𝒌=𝑺𝒖𝒏𝒏𝒚, 𝑻𝒆𝒎𝒑𝒆𝒓𝒂𝒕𝒖𝒓𝒆=𝑪𝒐𝒐𝒍, 𝑯𝒖𝒎𝒊𝒅𝒊𝒕𝒚=𝑯𝒊𝒈𝒉, 𝑾𝒊𝒏𝒅=𝑺𝒕𝒓𝒐𝒏𝒈)

that will have to be classified (i.e., are we going to play tennis under the conditions specified by 𝑋^′).

With the MAP rule, we compute the posterior probabilities.

This is easily done by looking up the tables we built in the learning phase.

Naïve Bayes Classifier

Naïve Bayes is a conditional probability model: given a problem instance to be classified, represented by a
representing some features (independent variables), it assigns to this instance probabilities for each of possible outcomes or classes .

The problem with the above formulation is that if the number of features is large or if a feature can take on a large number of values, then basing such a model on probability tables is infeasible. The model must therefore be reformulated to make it more tractable. Using Bayes' theorem, the conditional probability can be decomposed as

In plain English, using Bayesian probability terminology, the above equation can be written as

In practice, there is interest only in the numerator of that fraction, because the denominator does not depend on and the values of the features are given, so that the denominator is effectively constant. The numerator is equivalent to the joint probability model

Which can be rewritten as follows, using the chain rule for repeated applications of the definition of conditional probability

Now the "Naïve" conditional independence assumptions come into play: assume that all features in are mutually independent, conditional on the category .

Under this assumption,

Thus, the joint model can be expressed as

where

denotes proportionality.

This means that under the above independence assumptions, the conditional distribution over the class is:

where the evidence

is a scaling factor dependent only on

Constructing a classifier from the probability model

The Naïve Bayes classifier combines this model with a decision rule. One common rule is to pick the hypothesis that is most probable so as to this minimize the probability of misclassification; this is known as the maximum a posteriori or MAP decision rule.

The corresponding classifier, a Bayes classifier, is the function that assigns a class label for some as follows:

Naïve Bayes Classifier - ML Program

Naïve Bayes Classifier

Steps:

Understand the business problem
Import the library files
Load the dataset
Data preprocessing
Split the data into train and test
Build the model (Naïve Bayes classifier)
Test the model
Performance Measures
Predict the class label for new data.

1. Understand the business problem

Let’s build a classifier that predicts whether I should play tennis given the forecast. It takes four attributes to describe the forecast; namely, the outlook, the temperature, the humidity, and the presence or absence of wind. Furthermore, the values of the four attributes are qualitative (also known as categorical).

p(C_k |x_1,x_2,…,x_n )= p(C_k ) ∏_(i=1)^n p(x_i |C_k )